

It is possible that even if the treatment has no effect, we could get a mean score of 540. Since we are only interested in whether or not the pill has a positive effect, we are doing a one-tailed Z-Test, and our null hypothesis is:įinally, we have to choose a level of significance (α) for our test. The null hypothesis, denoted H₀, is always that the statistic measures of the treated group (in this case students given a pill) is the same as that for the general population.
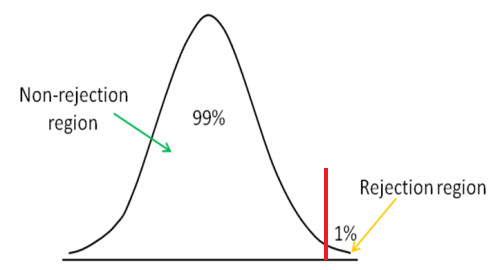
In inferential statistics, there are two hypothesis, the null hypothesis, and the alternative hypothesis. Given that the average score of all high school seniors on the SAT is μ = 510 with standard deviation σ = 100, is there statistically significant evidence that students who took the pill scored higher?īefore beginning the calculations, it is necessary to come up with specific hypotheses for the tests and choose a level of significance. The average score of student who took the pill is x̄ = 540. After being administered the pill, subjects take the SAT, and their scores on the SAT Math section are tabulated.
#One tailed hypothesis test calculator how to
This tutorial demonstrates how to use your graphing calculator to solve basic hypothesis testing problems such as the following using the Z-Test:Ī researcher designs an experiment where a random sample of n = 50 high school seniors are given a pill to improve their concentration and problem solving skills. With the statistics package installed, the TI-89, TI-92 Plus, and Voyage 200 also have much of this capability.
#One tailed hypothesis test calculator plus
The TI-83 Plus and TI-84 Plus are optimized for performing many tasks in statistics, and one of their most powerful features is the ability to perform a variety of tests of statistical significance.


 0 kommentar(er)
0 kommentar(er)
